Answer:
100π units square
Explanation:
The circle is centered on the point (-1,5) and contains the point (7,11).
We can find the radius, using the distance formula,
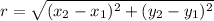
We substitute the points to get:
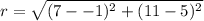
This implies that:
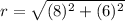
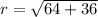

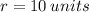
The area of a circle is given by:
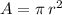
Plug in the radius into the formula to get:
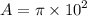
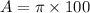
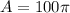
The area is 100π square units or 314 square units