Question

Trigonometry

Arc Length and Radian Measure
Solve the following problem.
Convert 55* to radians.

Answer 1

0.96 radians

Explanation:

Degrees : radians

180 : pi

55 : x

x/55 = pi/180

x = 55pi/180

x = 11pi/36

x = 0.96 radians

Answer 2

55° is equal to 0.9599 radians.

Step-by-step explanation:

Step 1:

If an angle is represented in degrees, it will be of the form x°.

If an angle is represented in radians, it will be of the form
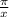`(\pi)/(x)`radians.

To convert degrees to radians, we multiply the degree measure by
`(\pi)/(180)`.

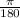For the conversion of degrees to radians,

the degrees in radians = (given value in degrees)(
`(\pi)/(180)`).

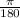Step 2:

To convert 50°,

`55\left((\pi)/(180)\right)=(55\pi)/(180).`

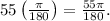
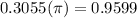`0.3055 (\pi) =0.9599` radians.

So 55° is equal to 0.9599 radians.