Question

Jack looks at a clock tower from a distance and determines that the angle of elevation of the top of the tower is 40°. John, who is standing 20 meters from Jack as shown in the diagram, determines that the angle of elevation to the top of the tower is 60°. If Jack's and John's eyes are 1.5 meters from the ground and the distance from Jack's eyes to the top of the tower is 50.64 meters, how far is John from the base of the tower? Round your answer to the nearest tenth.

A.
24.5 meters

B.
16.1 meters

C.
22.2 meters

D.
18.8 meters

Answer 1

18.7939 m

Explanation:

-Let x be the distance between John and clock tower.

-Let y be the vertical distance from the eyes of the two men standing to the top of the clock tower.

#Taking the right triangle ACD:

`\Tan \ theta=(Perpendicular \ Height)/(Base)\\\\Tan \ 60\textdegree=(y+1.5)/(x)\\\\y=x \ Tan \ 60\textdegree -1.5`

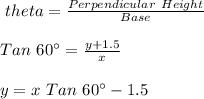
#Taking the right triangle ABD:

`\Tan \ theta=(Perpendicular \ Height)/(Base)\\\\Tan \ 40\textdegree=(y+1.5)/(x+20)\\\\y=(x+20)\ Tan \ 40\textdegree -1.5`

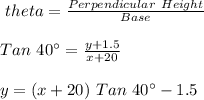
#We equate the two yo solve for x and y;

`(x+20)\ Tan \ 40\textdegree -1.5=x\ Tan \ 60\textdegree -1.5\\\\(x+20)\ Tan \ 40\textdegree=x\ Tan \ 60\textdegree\\\\0.8391x+16.7820=1.7321x\\\\x=18.7939`

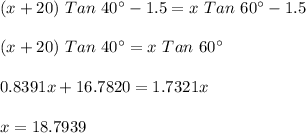
Hence, John's distance from the tower's base is 18.7939 m