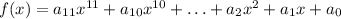Question

According to the fundamental Theorem of algebra, which polynomial function has exactly 11 roots?

Answer 1

f(x) = (x+2)³(x²−7x+3)⁴ or the second option

Step-by-step explanation:

just took the test

Answer 2

Step-by-step explanation:

The Fundamental Theorem of Algebra states the following:

For any polynomial of degree n we will have n roots.

So the general form of the equation of a polynomial is:

`A \ \mathbf{polynomial \ function} \ of \ x \ with \ degree \ n \ is \ given \ by:\\ \\ f(x)=a_(n)x^(n)+a_(n-1)x^(n-1)+\ldots +a_(2)x^(2)+a_(1)x+a_(0) \\ \\ where \ n \ is \ a \ nonnegative \ integer \ and \ a_(n), a_(n-1), \ldots a_(2), a_(1), a_(0) \\ with \ a_(n)\\eq`

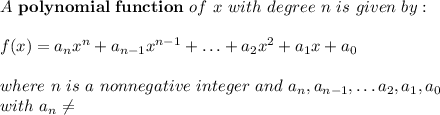
Since our polynomial will have exactly 11 roots, then the equation will have the following form:

`f(x)=a_(11)x^(11)+a_(10)x^(10)+\ldots +a_(2)x^(2)+a_(1)x+a_(0)`