Question

In the diagram, the radius of the outer circle is

2x cm and the radius of the inside circle is 6
cm. The area of the shaded region is
2887 cm?
What is the value of x?
Enter your answer in the box
x =
cm

Answer 1

the value of x is 8 cm.

Explanation:

Correct Question : In the diagram, the radius of the outer circle is 2x cm and the radius of the inside circle is 6 cm. The area of the shaded region is 220π cm2. What is the value of x? Enter your answer in the box.

We have ,

the area of a circle = πr²

the outer circle area =
`\pi(2x)^2 =4\pi x^2`

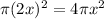
the inside circle area =
`\pi (6)^2= 36\pi`

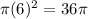
According to Question,

the outer circle area - the inside circle area = he shaded region

⇒
`\pi (4x^2)-36\pi =220\pi`

⇒
`x^2-9 =55`

⇒
`x^2=64`

⇒
`x =√(64)=8`

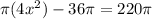
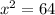
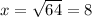
Therefore , the value of x is 8 cm.