Question

Can anybody help me with trying to figure out how to do this?

Answer 1

a. Angle A = 35

As triangle ABD has angle ADB equal to 90°

=> ABD is the right triangle

=> Angle ABD + Angel A = 90°

=> Angel A = 90° - Angel ABD = 90°- 55° = 35°

So Angel A = 35°

b. Angle CBD = 61

As triangle BDC has angle BDC equal to 90°

=> BDC is the right triangle

=> Angle CBD + Angel C = 90°

=> Angel CBD = 90° - Angel C = 90°- 29° = 61°

So Angel CBD = 61°

c. AD = 32.77

As ABD is the right triangle, so that we have the formula:

sin (an angel) = opposite side/ hypotenuse

=> sin angel ABD = AD/ AB

=> AD = sin angel ABD x AB = sin 55° x 40 ≈ 32.77

So AD = 32.77

d. BC = 47.32

As ABD is the right triangle, according to Pythagoras theorem, we have:

`BD^(2) = AB^(2) -AD^(2) =40^(2) - 32.77^(2) = 1600-1073.8729 = 526.1271`

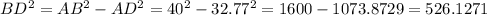
=> BD ≈ 22.94

As BCD is the right triangle, so that we have the formula:

sin (an angel) = opposite side/ hypotenuse

=> sin angel C = BD/ BC

=> BC = BD/ sin angel C = 22.94 / sin 29° ≈ 47.32

So BC = 47.32

e. CD = 41.39

As BCD is the right triangle, according to Pythagoras theorem, we have:
`CD^(2) = BC^(2) - BD^(2) =47.32^(2) -526.1271= 2239.1824-526.1271=1713.0553`

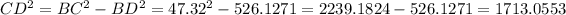
=> CD ≈ 41.39

f. BD = 22. 94 (part d)