Answer:
Explanation:
In order to find out how long it takes the ball to reach its max height, we will find the velocity function (the first derivative of the position function) and then set it equal to 0, since an object at its max height has to stop in the air in order to turn around and come back down. If
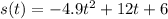 , then the first derivative, the velocity function, is
, then the first derivative, the velocity function, is
v(t) = -9.8t + 12 and setting it equal to 0,
0 = -9.8t + 12 and
9.8t = 12 so
t = 1.224 seconds
You could find the max height by subbing the time it takes to reach its max height into the position function:
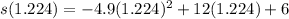 to get that the max height,
to get that the max height,
s(1.224) = 13.35 meters