Answer:
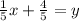
Explanation:
f(x) = 5x-4
1. First, you want to rewrite the function with x and y
y= 5x-4
2. Then, switch the variables x and y
x= 5y-4
3. Now, solve for y.
x= 5y-4
x+4 = 5y
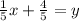 --> This is your inverse.
--> This is your inverse.
To check:
You can check this answer by plugging your inverse into your original function. You will know that your inverse is correct if your answer is x = 1
1. y= 5x-4,
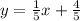
2. Since they both equal to y, pick one equation to plug into the other. In this case, you are simply setting them equal to each other.
5x-4 =
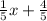
3. Solve for x.
5x-4 =
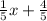
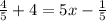
24=24x
x=1
4. Since you reached the answer x=1, you didn't get any extraneous solutions and your answer is therefore correct.