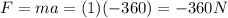Question

A.) Calculate the recoil velocity of a 1. kg plunger that directly interacts with a .02kg bullet fired at 600 meters/second

B.) If this part were to be stopped over 20.Cm, what would the ForceAvg. be on the gun?

Answer 1

A) -12 m/s

B) -360 N

Step-by-step explanation:

A)

We can solve this problem by using the law of conservation of momentum: in fact, the total momentum of the plunger + bullet system must be conserved.

Initially, their total momentum is zero, since they are at rest:

`p_i=0`

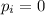
While the final total momentum is

`p_f=mv+MV`

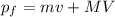
where:

m = 0.02 kg is the mass of the bullet

v = 600 m/s is the velocity of the bullet

M = 1 kg is the mass of the plunger

V is the recoil velocity of the plunger

Since momentum is conserved,

`p_i=p_f`

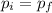
And so we find V:

`0=mv+MV\\V=-(mv)/(M)=-((0.02)(600))/(1)=-12 m/s`

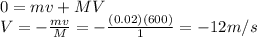
B)

From part A), we said that the speed of the plunger after the shot is

u = 12 m/s

In order to be stopped, its final velocity must be

v = 0

Since its an accelerated motion, we can find its acceleration using the suvat equation

`v^2-u^2=2as`

where

s = 20 cm = 0.20 m is the stopping distance

Solving for the acceleration, we find

`a=(v^2-u^2)/(2s)=(0-12^2)/(2(0.20))=-360 m/s^2`

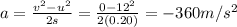
And since the mass of the plunger is

m = 1 kg

The force on it would be (Newton's second law)

`F=ma=(1)(-360)=-360 N`