Question

Suppose that there are two types of tickets to a show: advance and same-day. The combined cost of one advance ticket and one same-day ticket is $35. For one performance, 40 advance tickets and 25 same-day tickets were sold. The total amount paid for the tickets was $1100. What was the price of each kind of ticket?

Answer 1

Advance tickets-$15

Same-day tickets-$20

Explanation:

let x be the cost of advance tickets and y cost of same-day tickets:

`x+y=35\ \ \ \ \ \ \ ...i`

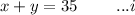
Given that there were 40 advance and 25 same-day tickets for a total of $1100:

`40x+25y=1100\\\\8x+5y=220\ \ \ \ \ \ \ \ \ \ \ ...ii`

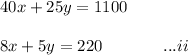
#Make x the subject in i and substitute in ii:

`x=35-y\\\\\therefore 8x+5y=220, x=35-y\\\\8(35-y)+5y=220\\\\280-8y+5y=220\\\\60=3y\\\\y=20\\\\x=35-y=35-20=15`

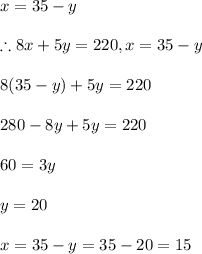
Hence, advance tickets cost $15 each while same-day tickets cost $20 each.