Step-by-step explanation:
In every rectangle, the two diagonals have the same length. If a quadrilateral's diagonals have the same length, that doesn't mean it has to be a rectangle, but if a parallelogram's diagonals have the same length, then it's definitely a rectangle.
So first of all, let's prove this is a parallelogram. The basic definition of a parallelogram is that it is a quadrilateral where both pairs of opposite sides are parallel.
So let's name the vertices as:

First pair of opposite sides:
Slope:
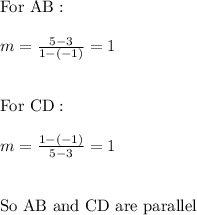
Second pair of opposite sides:
Slope:
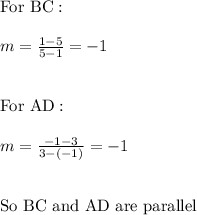
So in fact this is a parallelogram. The other thing we need to prove is that the diagonals measure the same. Using distance formula:
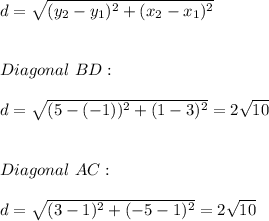
So the diagonals measure the same, therefore this is a rectangle.