Question

The vertices of triangle XYZ are x [-6,-4]y [-10,-2] z [-6,-2] What is the approximate perimeter of the triangle?

Answer 1

The approximate perimeter of the triangle is 10.5 units

Explanation:

we know that

The perimeter of triangle is equal to the sum of its three length sides

so

`P=XY+YZ+XZ`

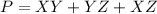
the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

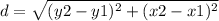
step 1

Find the distance XY

we have

x [-6,-4], y [-10,-2]

substitute in the formula

`d=\sqrt{(-2+4)^(2)+(-10+6)^(2)}`

`d=\sqrt{(2)^(2)+(-4)^(2)}`

`d_X_Y=√(20)\ units`

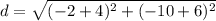
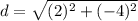
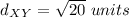
step 2

Find the distance YZ

we have

y [-10,-2], z [-6,-2]

substitute in the formula

`d=\sqrt{(-2+2)^(2)+(-6+10)^(2)}`

`d=\sqrt{(0)^(2)+(4)^(2)}`

`d_Y_Z=4\ units`

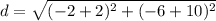
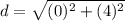
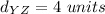
step 3

Find the distance XZ

we have

x [-6,-4], z [-6,-2]

substitute in the formula

`d=\sqrt{(-2+4)^(2)+(-6+6)^(2)}`

`d=\sqrt{(2)^(2)+(0)^(2)}`

`d_X_Z=2\ units`

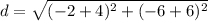
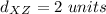
step 4

Find the perimeter

`P=XY+YZ+XZ`

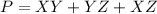
substitute

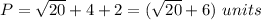`P=√(20)+4+2=(√(20)+6)\ units` ----> exact value

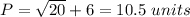`P=√(20)+6=10.5\ units` ----> approximate value