Question

Solve each inequality. Round to the nearest hundredth. 3x2 – 4 ≤ 6 – 5x

Answer 1

`x\in[-2.84,1.17]`

Explanation:

The first, we will write our inequality in another form:

`3x^2-4\leq 6-5x`

`3x^2-4-6+5x\leq 0`

`3x^2+5x-10\leq 0`

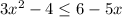
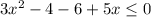
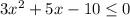
We want to know when is it equal to 0.

First we solve the equation
`3x^2+5x-10=0`:

`x_(1,2)=(-5+-√(25+120))/(6)`

`x_(1,2)=(-5+-12.04)/(6)`

`x_1=1.17`

`x_2=-2.84`

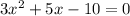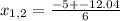
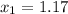
So we want to know when
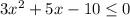`3x^2+5x-10\leq 0` is true. We know, when a>0 function is negative when x is between two zeros. In our example a=3>0. Then we have:

It is true if
`x\in[-2.84,1.17]`