a=4 , b=3 These values make the equation true .
Explanation:
Here we have , If a and b are both integers and b does not equal 0, then -(a/b) = (-a)/b = a/(-b) Choose two values for a and b. We need to find if those values make the equation true . Let's find out:
We have the following equation:
-(a/b) = (-a)/b = a/(-b) , Let a=4 , b=3 , So
⇒
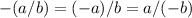
⇒
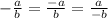
⇒
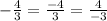
⇒
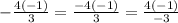 { Multiplying by -1 }
{ Multiplying by -1 }
⇒
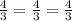
Therefore , These values make the equation true .