Answer:
An explicit expression is equal to 3m/8
Explanation:
we know that
Function T gives the time the Hobbits have to prepare for the attack, T(k), in minutes, as a function of troll's distance, k, in meters
so
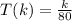
Function V gives visibility from the watchtower, V(m), in meters, as a function of the height of the watchtower, m, in meters
so
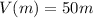
Find the composite figure
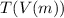
That will give the time the Hobbits have to prepare for the troll attack as a function of the height, m, of the watchtower
Substitute the variable k in the function T by the function V(m)

simplify
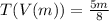
therefore
An explicit expression is equal to 3m/8