Question

Rajah

dilukis
selari
> menunjukkan garis
pada suatu satah
dengan CD.
lurus AB dan co yg
Castesan AB adalah
A
C(-2,0)
D(0,- 4)
B(-3,-5)
(a) Persamaan
garis
lurus AB
b) pintasan
-x
garis
lurus
AB​

Answer 1

The equation of a straight line AB is y = -2x - 11.

The x-intercept of the line is
`-(11)/(2)`.

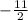Solution:

Given data:

C(-2, 0) and D(0, -4)

Slope of CD:

`$m=(y_2-y_1)/(x_2-x_1)`

`$m=(-4-0)/(0-(-2))`

`$m=(-4)/(2)`

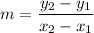
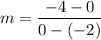
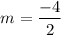
m = -2

AB and CD are parallel lines.

If two lines are parallel then their slopes are equal.

Therefore slope of AB = -2

AB passes through the point (-3, -5).

Point-slope formula:

`y-y_1=m(x-x_1)`

Here, m = -2 and
`x_1=-3, y_1=-5`

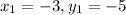
y - (-5) = -2(x - (-3))

y + 5 = -2(x + 3)

y + 5 = -2x - 6

Subtract 5 on both sides, we get

y = -2x - 11

The equation of a straight line AB is y = -2x - 11.

To find the x-intercept,substitute y = 0 in the equation of a line.

0 = -2x - 11

Add 11 on both sides.

11 = -2x

Divide by -2 on both sides.

`$-(11)/(2)=x`

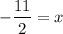
The x-intercept of the line is
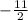`-(11)/(2)`.