angles formed by these tosses are
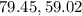 and
and
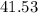 degrees to the nearest hundredth.
degrees to the nearest hundredth.
Explanation:
Here , We have a triangle with sides of length 8.6 feet, 5.8 feet and 7.5 feet.
The Law of Cosines (also called the Cosine Rule) says:
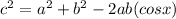
Using the Cosine Rule to find the measure of the angle opposite the side of length 8.6 feet:
⇒
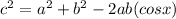
⇒
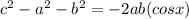
⇒
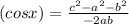
⇒
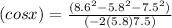
⇒
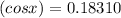
⇒
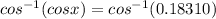
⇒
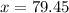
The Law of Sines (or Sine Rule) is very useful for solving triangles:
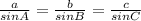
We can now find another angle using the sine rule:
⇒
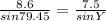
⇒
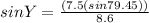
⇒
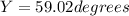
So, the third angle =
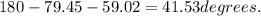
Therefore, angles formed by these tosses are
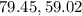 and
and
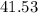 degrees to the nearest hundredth.
degrees to the nearest hundredth.