Answer:
So the radius is increasing at
 .
.
This is approximately 0.00497 cm/min that the radius is increasing.
Explanation:
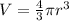
The volume and radius are both things that are changing with respect to time.
So their derivatives will definitely not be 0.
Let's differentiate:
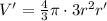
I had to use constant multiple rule and chain rule.
We are given
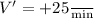 and
and
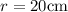 .
.
We want to find
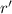 .
.
Let's plug in first:

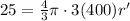
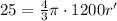
Multiply both sides by 3:
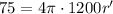
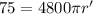
Divide both sides by
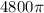 :
:
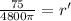
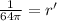
So the radius is increasing at
 .
.
This is approximately 0.00497 cm/min that the radius is increasing.