Question

Find the x and y intercepts of the function f (x) = 2x^2 - 7x + 5

Answer 1

x-intercepts at x = 1 and 2.5

y-intercept at y = 5

Explanation:

Given: f(x) = 2x² - 7x + 5

It is required to find x and y intercepts.

x-intercept ⇒ the value of x when y = 0

y-intercept ⇒ the value of y when x = 0

So, to find x intercepts of the given function put f(x) = 0

∴ 2x² - 7x + 5 = 0

a = 2 , b = -7 and c = 5

Using the general rule to find the roots:

`x=(-b \pm √(b^2-4ac) )/(2a) =(-(-7) \pm √((-7)^2-4*2*5) )/(2*2) =(7 \pm √(49-40) )/(4)=(7 \pm √(9) )/(4)=(7 \pm 3 )/(4)`

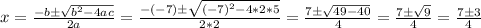
∴ x = (7+3)/2 = 10/2 = 2.5

OR x = (7-3)/4 = 4/4 = 1

So, x-intercepts at x = 1 and 2.5

===========================================

To find y intercepts of the given function put x = 0

∴ y = 2x² - 7x + 5 = 2 * (0)² - 7 * 0 + 5 = 5

So, y-intercept at y = 5

============================================

See the attached figure which represents x and y intercepts of the function f(x) using the graph.