Answer:
A. Perimeter
B. Sides
D. Area
Explanation:
Suppose a triangle ABC has sides each of length a
formula:
The altitude of the triangle h equal to :
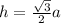
________
Perimeter:
Let’s P be the perimeter of the triangle ABC then P = 3a
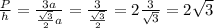
P/h is a constant then The perimeter has a proportional relationship to the altitude
______
Sides :
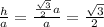
h/a is a constant then The side has a proportional relationship to the altitude
______
Area :
Let A be the area of the triangle
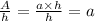
A/h is a constant then The area has a proportional relationship to the altitude
_____
Angles :
The measure Of each angle of an equilateral triangle is always equal to 60°
60/h is not a constant then there is no proportional relationship
______
Vertices:
The vertices are points and not numbers so there is no proportional relationship.