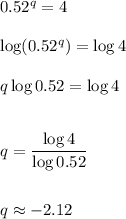Question

Solving Exponential Equations (lacking a common base)

(0.52)^9=4

Answer 1

q= -2.584

Step-by-step explanation:

(0.52)^q = 4.

We exponent are written in compound forms, having a different base, we solve such taking the logs of both sides of the equation.

(0.52)^q = 4

We take the log of both sides!

q * log 0.52 = log 4.

q * -0.284 = 0.602

Divide through by -0.233

q = 0.602/ - 0.233

q = -2.584

Answer 2

`q\approx-2.12`

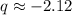
Step-by-step explanation:

The exponent of 0.52 is not 9 but q. Thus, you need so solve the equattion to find the value of the exponent, q.

To solve exponential equations with different bases, you must use logarithms, which is the inverse function of exponentiation:

`0.52^q=4\\\\\log (0.52^q)=\log 4\\\\q\log 0.52=\log 4\\\\\\q=(\log 4)/(\log 0.52)\\\\\\q\approx-2.12`