Part A r =
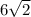 units & h = 2 units:
units & h = 2 units:
Explanation:
Here we have , cones A and B both have volume 48(3.14) cubic units but they have different dimensions. Cone A has radius 6 units and height 4 units. We need to find:
Part A
Find one possible radius and height for Cone B.
Since , volume of cone A and B are same so ,
Volume of cone A =
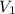 , Volume of cone V =
, Volume of cone V =
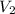
By hit & trial , One possible radius and height for Cone B is r =
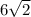 units & h = 2 units:
units & h = 2 units:
⇒

⇒
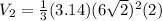
⇒
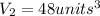
Part B
Explain how you know Cone B has the same volume as Cone A.
Volume of cone A =
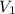 :
:
Cone A has radius 6 units and height 4 units, So
⇒
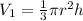
⇒
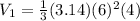
⇒
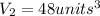
Volume of cone V =
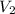
⇒

⇒
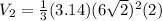
⇒
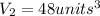
Hence, Volume of both are same!