Answer:
![\sqrt[n]{a} =a^{(1)/(n)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/83pv4vhha0grvwq4xauv47gbacmbgwove1.png)
Step-by-step explanation:
Roots of real numbers can be represented by radicals or by exponents.
First, I present some examples to show how exponents and radicals are related, and then generalize.
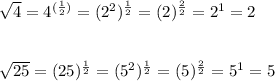
![\sqrt[3]{8}=(8)^{(1)/(3)}=(2^3)^{(1)/(3)}=(2)^{(3)/(3)}=2^1=2](https://img.qammunity.org/2021/formulas/mathematics/middle-school/817nft2px5j26sc4l0go3ldn1umedbyswm.png)
When you write 5² = 25, then 5 is the square root of 25.
And in general, if n is a positive integer and
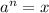 , then
, then
 is the nth root of x.
is the nth root of x.
Also, if n even (and positive) and
 is positive, then
is positive, then
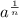 is the positive nth root of
is the positive nth root of

Thus,
![\sqrt[n]{a} =a^{(1)/(n)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/83pv4vhha0grvwq4xauv47gbacmbgwove1.png)