Step-by-step explanation:
The least common denominator (LCD) is defined as the least common multiple of the denominators of a set of fractions. In this case, we have the fractions:

So the LCD here is the product of
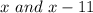 . Therefore:
. Therefore:
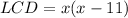
So we can write equivalent expressions as:

As you can see, both expression has the same denominator which is the LCD.