Question

An envelope measures 5 inches by 12 inches. A pencil is placed in the envelope at a diagonal. What is the maximum possible lenght of the pencil?

Answer 1

the maximum possible length of the pencil is 13 inches

Explanation:

Here we have , An envelope measures 5 inches by 12 inches. A pencil is placed in the envelope at a diagonal. We need to find What is the maximum possible length of the pencil . Let's find out:

We know that maximum length which can be fitted in envelope will be the length of diagonal of envelope . So

By Pythagoras theorem

`Diagonal^2 = length^2 +breadth^2`

⇒
`Diagonal^2 = length^2 +breadth^2`

⇒
`Diagonal^2 =5^2 +12^2`

⇒
`Diagonal^2 =25 +144`

⇒
`Diagonal^2 = 169`

⇒
`√(Diagonal^2) = √(169)`

⇒
`Diagonal= 13 inch`

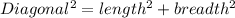
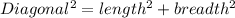
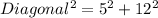
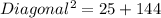
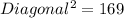
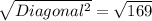
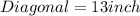
Therefore, the maximum possible length of the pencil is 13 inches .