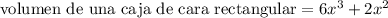Question

Teniendo en cuenta que el volumen de una caja de cara rectangular es igual al producto del largo 2x , por el ancho x, por el alto 3x+1 . ¿cual es el volumen de la caja?

Answer 1

Por lo tanto,

Volumen de la caja ,

`\textrm{volumen de una caja de cara rectangular}=6x^(3)+2x^(2)`

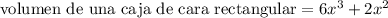
Explanation:

Dado:

El volumen de una caja rectangular viene dado por

`\textrm{volumen de una caja de cara rectangular}=2x* x* (3x+1)`

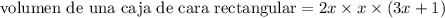
Encontrar:

Volumen de la caja = ?

Solución:

Volumen de una caja rectangular,

`\textrm{volumen de una caja rectangular}=Longitud* Anchura* Altura`

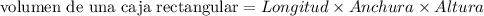
Aquí se da que,

`\textrm{volumen de una caja de cara rectangular}=2x* x* (3x+1)`

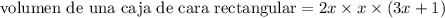
Aplicación de la propiedad distributiva A (B + C) = AB + AC

`\textrm{volumen de una caja de cara rectangular}=2x^(2)(3x+1)\\\textrm{volumen de una caja de cara rectangular}=2x^(2)* 3x+2x^(2)* 1\\\textrm{volumen de una caja de cara rectangular}=6x^(3)+2x^(2)`

Por lo tanto,

Volumen de la caja ,

`\textrm{volumen de una caja de cara rectangular}=6x^(3)+2x^(2)`