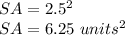Answer:
Part 1)
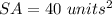
Part 2)
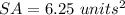
Explanation:
Part 1) we know that
The surface area of a square pyramid is equal to the area of the square base plus the area of its four triangular faces
so
![SA=b^2+4[(1)/(2)(b)(h)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/khc67vnomhwqq1z3zuib825phxexbr8yjl.png)
we have
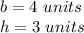
substitute
![SA=4^2+4[(1)/(2)(4)(3)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/seheaj7jf451pys23m267hp97f1j5zq3o0.png)
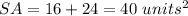
Part 2) we know that
The surface are of the cube is equal to the area of its six square faces
so
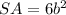
we have
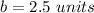
substitute