Question

I need help on my homework, please help!!

The graph of the function y=(1/2)^x is shown at right.

a. Describe what happens to y as x gets larger and larger. For example, what is y when x=20? x=100? x=1000? x=n(a much larger number)?

b. Does the graph of y=(1/2)^x have an x‑intercept? Explain how you know.

c. Does y=(1/2)^x have a vertical asymptote? In other words, is there a vertical line that the graph above approaches? Why or why not?

Answer 1

a) y approaches zero

b) The graph has no x-intercept

c) The graph does not have vertical asymptote.

Explanation:

The given function is

`y = { ((1)/(2)) }^(x)`

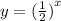
When x=20,

`y = \frac{1}{ {2}^(20) }`

when x=100,

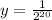
`y = \frac{1}{ {2}^(100) }`

When x=1000,

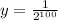
`y = \frac{1}{ {2}^(1000) }`

As x is getting larger, y is approaching zero.

b) The graph of

`y = { ((1)/(2)) }^(x)`

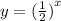
does not have x-intercepts.

Because when y=0, we get:

`0 = { ((1)/(2) )}^(x)`

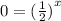
This gives us:

`0 = 1`

Which is false.

Meaning the graph has no x-intercept , it is asymptotic to the x-axis.

c) The graph does not have a vertical asymptote.

For a vertical asymptote, the denominator of the function is zero.

`y = \frac{1}{ {2}^(x) }`

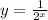
So

`{2}^(x) = 0`

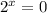
But we know that an exponential function is never zero.

Therefore the graph has no vertical asymptote