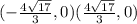Question

What are the foci of the ellipse 8x^2+9y^2=96

Answer 1

Explanation:

Let's first get this into standard form of an ellipse. That means that we divide everything by 96 so we have a 1 on the right side of the equals sign:

`(8x^2)/(96)+(9y^2)/(96)=1`

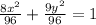
Doing the division simplifies this down to

`(x^2)/(12)+(y^2)/((32)/(3) )=1`

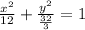
We know from the numerators that this is an ellipse centered about the origin (its center is (0, 0).

To find the coordinates of the foci, use

`c^2=a^2-b^2`

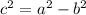
For an ellipse, a is always larger than b, and the larger number is always under the x-term. So we have a horizontally oriented ellipse. Our a = 12 and b = 32/3. Filling in our equation:

`c^2=12^2-((32)/(3))^2`

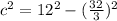
and

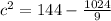`c^2=144-(1024)/(9)` and

`c^2=(272)/(9)`

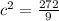
Taking the square root of both sides and simplifying in the process gives you that

`c=+/-(4√(17) )/(3)`

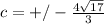
So the coordinates of the foci are

`(-(4√(17) )/(3),0)((4√(17) )/(3),0)`