Answer:
ln(3) + 5 - 3ln(x) or 6.0986 - 3ln(x)
Explanation:

 =
=
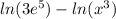 , since ln(x/y) = ln(x)-ln(y)
, since ln(x/y) = ln(x)-ln(y)
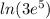 = ln(3) +
= ln(3) +
 , since ln(xy) = ln(x) + ln(y)
, since ln(xy) = ln(x) + ln(y)
 = ln(3) +
= ln(3) +

 =
=
 , since ln(
, since ln(
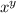 ) = yln(x)
) = yln(x)
 = ln(3) + 5 -3ln(x) , since ln(e)=1
= ln(3) + 5 -3ln(x) , since ln(e)=1
if needed further simplification,
ln(3) = 1.0986
ln(e) = 1
 = 6.0986 - 3ln(x)
= 6.0986 - 3ln(x)