Answer:
0.2700
Explanation:
-Notice that this is a binomial distribution with p=0.52, n=4 and x=3.
-The formula for the binomial probabilities is given as:
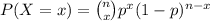
The probability than in 4, exactly 3 order their food on the go is:
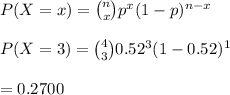
Hence, the probability that exactly 3 order their food on the go is 0.2700