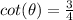Question

suppose theta is an angle in the standard position whose terminal side is in Quadrant 1 and sin theta = S4/S5. find the exact values of the five remaining trig functions of theta

Answer 1

`csc(\theta)=(5)/(4)`

`cos(\theta)=(3)/(5)`

`sec(\theta)=(5)/(3)`

`tan(\theta)=(4)/(3)`

`cot(\theta)=(3)/(4)`

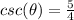
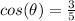
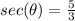
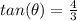
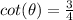
Explanation:

step 1

Find the
`csc(\theta)`

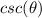
we know that

`csc(\theta)=(1)/(sin(\theta))`

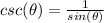
we have

`sin(\theta)=(4)/(5)`

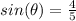
therefore

`csc(\theta)=(5)/(4)`

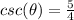
step 2

Find the
`cos(\theta)`

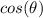
we know that

`sin^2(\theta)+cos^2(\theta)=1`

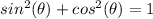
we have

`sin(\theta)=(4)/(5)`

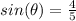
substitute

`((4)/(5))^2+cos^2(\theta)=1`

`cos^2(\theta)=1-((4)/(5))^2`

`cos^2(\theta)=1-((16)/(25))`

`cos^2(\theta)=((9)/(25))`

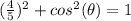
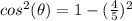
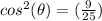
square root both sides

`cos(\theta)=\pm((3)/(5))`

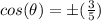
Remember that the angle theta is in quadrant I

so

The value of cosine of angle theta is positive

`cos(\theta)=(3)/(5)`

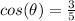
step 3

Find the
`sec(\theta)`

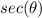
we know that

`sec(\theta)=(1)/(cos(\theta))`

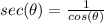
we have

`cos(\theta)=(3)/(5)`

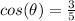
therefore

`sec(\theta)=(5)/(3)`

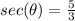
step 4

Find the value of
`tan(\theta)`

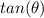
we know that

`tan(\theta)=(sin(\theta))/(cos(\theta))`

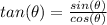
we have

`sin(\theta)=(4)/(5)`

`cos(\theta)=(3)/(5)`

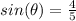
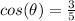
substitute the values

`tan(\theta)=(4)/(3)`

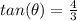
step 5

Find the value of
`cot(\theta)`

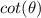
we know that

`cot(\theta)=(1)/(tan(\theta))`

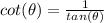
we have

`tan(\theta)=(4)/(3)`

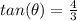
therefore

`cot(\theta)=(3)/(4)`