The power, in watts, dissipated as heat in a resistor varies jointly with the resistance, in ohms, and the square of the current, in amperes. A 15-ohm resistor carrying a curren…

Question

asked Jul 25, 2021 19.5k views

1 Answer

Snatchysquid · Answer 1 · 2021-07-29T06:44:56+0000

Answer:

The power dissipated is 45W.

Explanation:

The power
varies jointly with resistance
, and the square of current
:

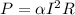$P = \alpha I^2R$ ,

where
$\alpha$ is the constant of proportionality.

Now we are told that when
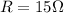$R = 15\Omega$ and
I =1A ,
P = 15W :

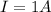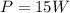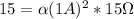
$15 = \alpha (1A)^2*15\Omega$

solving for
$\alpha$ we get

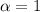$\alpha = 1$ ,

which gives

P = I^2R

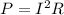
With the value of
$\alpha$ in hand, we find the power dissipated when
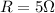$R =5\Omega$ and
I = 3 A:

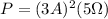
$P = (3A)^2(5\Omega )$

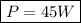
$\boxed{P =45W}$

Thus, the power dissipated is 45W.