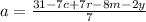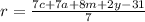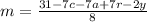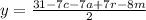Question

7c + 7a - 7r + 8m + 2y=31

solve for c a r m and y​

Answer 1

For this case we have the following equation:

`7c + 7a-7r + 8m + 2y = 31`

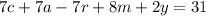
We solve for c:

We pass the terms that do not contain "c" to the other side of the equation by changing signs:

`7c = 31-7a + 7r-8m-2y`

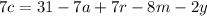
We divide by 7 on both sides of the equation:

`c = \frac {31-7a + 7r-8m-2y} {7}`

We solve for "a":

We pass the terms that do not contain "a" to the other side of the equation by changing signs:

`7a = 31-7c + 7r-8m-2y`

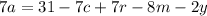
We divide by 7 on both sides of the equation:

`a = \frac {31-7c + 7r-8m-2y} {7}`

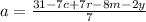
We solve for r:

We pass the terms that do not contain "r" to the other side of the equation by changing signs:

`-7r = 31-7c-7a-8m-2y`

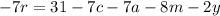
We multiply by -1 on both sides:

`7r = 7c + 7a + 8m + 2y-31`

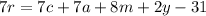
We divide by 7 on both sides of the equation:

`r = \frac {7c + 7a + 8m + 2y-31} {7}`

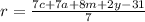
We solve for m:

We pass the terms that do not contain "m" to the other side of the equation by changing signs:

`7c + 7a-7r + 8m + 2y = 31\\8m = 31-7c-7a + 7r-2y`

We divide by 7 on both sides of the equation:

`m = \frac {31-7c-7a + 7r-2y} {8}`

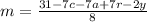
We solve for y:

We pass the terms that do not contain "y" to the other side of the equation by changing signs:

`2y=31-7c-7a+7r-8m`

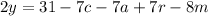
We divide by 2 on both sides of the equation:

`y=(31-7c-7a+7r-8m)/(2)`

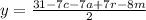
Answer:

`c = \frac {31-7a + 7r-8m-2y} {7}`

`a = \frac {31-7c + 7r-8m-2y} {7}`

`r = \frac {7c + 7a + 8m + 2y-31} {7}`

`m = \frac {31-7c-7a + 7r-2y} {8}`

`y=(31-7c-7a+7r-8m)/(2)`