Answer:
See attachment.
Explanation:
We want to graph the rational function;

The vertical asymptotes occur at where the denominator is zero.

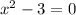
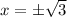
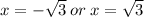
The horizontal asymptote is y=0, since the degree of the numerator is less than the degree of the denominator.
The y-intercept is
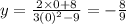
The x-intercept is

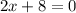
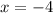
With this information we can graph the function as shown in attachment.