Graph the following rational functions

Question

asked Jul 4, 2021 99.4k views

1 Answer

Telmo Ivo · Answer 1 · 2021-07-09T04:45:23+0000

Answer:

See attachment.

Explanation:

We want to graph the rational function;

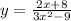
$y = \frac{2x + 8}{3 {x}^(2) - 9 }$

The vertical asymptotes occur at where the denominator is zero.

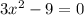
$3 {x}^(2) - 9 = 0$

${x}^(2) - 3 = 0$

$x = \pm √(3)$

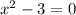
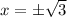
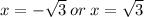
$x = - √(3) \: or \: x = √(3)$

The horizontal asymptote is y=0, since the degree of the numerator is less than the degree of the denominator.

The y-intercept is

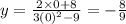
$y = \frac{2 * 0 + 8}{3 {(0)}^(2) - 9 } = - (8)/(9)$

The x-intercept is

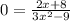
$0= \frac{2x + 8}{3 {x}^(2) - 9 }$

2x + 8 = 0

x = - 4

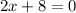
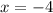
With this information we can graph the function as shown in attachment.