Question

One watering system needs about three times as long to complete a job as another warning system when both systems operate at the same time, the job can be completed in nine minutes. How long does it take in system to do the job

Answer 1

One watering system requires 36 minutes to complete the job alone while another watering system requires 12 minutes to complete the job alone.

Explanation:

Given:

Both the system can complete the job = 9 minutes

We need find the time required by each system to do the job.

Solution:

Let the time required by another watering system to complete the job be 'x' mins.

Now given:

One watering system needs about three times as long to complete a job as another watering system.

Time required by one watering system =
`3x`

Rate to complete the job by another watering system =
`(1)/(x)\ job/min`

Rate to complete the job by One watering system =
`(1)/(3x)\ job/min`

Rate at which both can complete the job =
`(1)/(9)\ job/min`

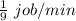
So we can say that;

Rate at which both can complete the job is equal to sum of Rate to complete the job by another watering system and Rate to complete the job by One watering system.

framing in equation form we get;

`(1)/(x)+(1)/(3x)=\frac19`

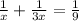
Now taking LCM to make the denominator common we get;

`(1*3)/(x* 3)+(1*1)/(3x*1)=\frac19\\\\(3)/(3x)+(1)/(3x)=\frac19\\\\(3+1)/(3x)=(1)/(9)\\\\(4)/(3x)=(1)/(9)`

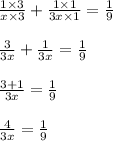
By Cross multiplication we get;

`4*9 =3x\\\\3x =36`

Dividing both side by 3 we get;

`(3x)/(3)=(36)/(3)\\\\x=12\ min`

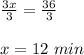
Time required by One watering system =
`3x =3* 12 =36\ min`

Hence One watering system requires 36 minutes to complete the job alone while another watering system requires 12 minutes to complete the job alone.