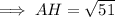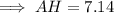Answer:
7.14 to the nearest hundreth
Explanation:
Using the Pythagorean Theorem,
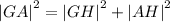
From the question,
GA=10
RA=7
Also, RA is parallel and equal to GH.
This implies that, RA=GH=7
By substitution we obtain,
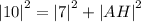
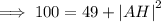
Subtracting 49 from both sides.
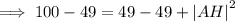

Taking positive square root of both sides.