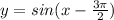Question

find a equation for a sinusoidal function that has period 2 pie amplitude 1 and contains the point 3 pie over 2, 0

Answer 1

Thus, the equation of sinusoidal function is
`y = sin( x - (3\pi )/(2) )`

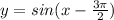
Step-by-step explanation:

The standard form of sine function is:

`y = asin[b(x-h)] + k`

where,

a = amplitude

2π/b = period

h = phase shift

k = vertical displacement

Step wise formation of the equation:

In sine curve, the basic model is:

y = sinx

Apply a vertical stretch/shrink to get the desired amplitude:

new equation:

y = a sin x

y = 1 sinx

For k > 0, the curve y = sin kx has period 2π/ k

The period is 2. So the value of k is

2π = 2π / b

b = 1

So, the equation becomes:

y = 1 sin x

Phase shift is 3π/2. The new equation is

`y = 1 sin [ 1 ( x - (3\pi )/(2) )]\\\\y = sin ( x - (3\pi )/(2))`

Vertical displacement, k = 0

So, the equation is

`y = sin ( x - (3\pi )/(2) ) + 0\\\\y = sin ( x - (3\pi )/(2))`

Thus, the equation of sinusoidal function is
`y = sin( x - (3\pi )/(2) )`