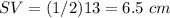Answer:
Part A) Option A. QR= 3 cm
Part B) Option B. SV=6.5 cm
Explanation:
step 1
Find the length of segment QR
we know that
If two triangles are similar, then the ratio of its corresponding sides is proportional and its corresponding angles are congruent
so
In this problem Triangle QRW and Triangle QSV are similar by AA Similarity Theorem
so

we have
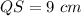 ---> because S is the midpoint QT (QS=TS)
---> because S is the midpoint QT (QS=TS)
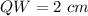 --->because V is the midpoint QU (QW+WV=VU)
--->because V is the midpoint QU (QW+WV=VU)
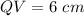 --->because V is the midpoint QU (QV=VU)
--->because V is the midpoint QU (QV=VU)
substitute the given values
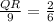
solve for QR

step 2
Find the length side SV
we know that
The Mid-segment Theorem states that the mid-segment connecting the midpoints of two sides of a triangle is parallel to the third side of the triangle, and the length of this mid-segment is half the length of the third side
so
In this problem
S is the mid-point side QT and V is the mid-point side QU
therefore
SV is parallel to TU
and
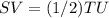
so