Answer:
The answer to your question is below
Explanation:
14a f(x) = (2x + 2)(5 - x²)
Process
1.- Factor (5 - x²)
(5 - x²) = (
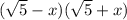
Then f(x) = (2x + 2) (
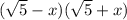
2.- Equal each factor to zero
2x₁ + 2 = 0
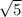 - x₂ = 0
- x₂ = 0
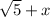 ₃ = 0
₃ = 0
2x₁ = -2 x₂ =
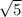 x₃ = -
x₃ = -
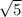
x₁ = -2/2
x₁ = -1
3.- Conclusion
The roots of the function are
x₁ = -1
x₂ =
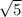
x₃ = -
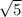
14b.Expand the function
(2x + 2) (5 - x²) = 10x - 2x³ + 10 - 2x²
or -2x³ - 2x² + 10x + 10