Answer:
The rate of change of the function is 2.
Explanation:
As we know that if the graph of a liner function passes through the two gives points on the coordinate plane, then the rate of change of the function will be the slope of the given line.
The points are:
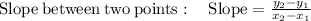
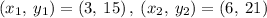
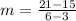
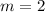
Therefore, the rate of change of the function is 2.