Question

One container is filled with mixture that is 25% acid. A second container is filled with a mixture that is 55% acid. The second container is 55% larger than the first, and the two containers are emptied into a third container. What percent of acid is the third container?

Answer 1

Therefore the third container contains
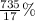`(735)/(17)\%` = 43.23 % acid.

Explanation:

Given that, One container is filled with the mixture that 25% acid. 55% acid is contain by second container.

Let the volume of first container be x cubic unit.

Since the volume of second container is 55% larger than the first.

Then the volume of the second container is

`= (V* (100+55)/(100))` cubic unit.

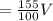`=(155)/(100)V` cubic unit.

The amount of acid in first container is

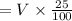`=V* (25)/(100)` cubic unit.

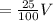`=(25)/(100)V` cubic unit.

The amount of acid in second container is

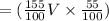`=((155)/(100)V * (55)/(100))` cubic unit.

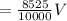`=(8525)/(10000)V` cubic unit.

Total amount of acid
`=((25)/(100)V+(8525)/(10000)V)` cubic unit.

`=((2500+8525)/(10000)V)` cubic unit.

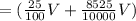`=((11025)/(10000)V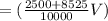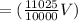)`cubic unit.

Total volume of mixture
`=(V+(155)/(100)V)` cubic unit.

`=(100+155)/(100)V` cubic unit.

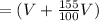`=(255)/(100)V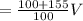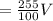` cubic unit.

The amount of acid in the mixture is

`=\frac{\textrm{The volume of acid}}{\textrm{The amount of mixture}}* 100 \%`

`=\frac {(11025)/(10000)V}{(255)/(100)V}* 100\%`

`=(735)/(17)\%`

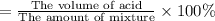
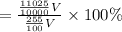
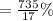
Therefore the third container contains
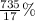`(735)/(17)\%` acid.