Question

Find the first five terms of the sequence in which a1 = –10 and an = 4an – 1 + 7, if n ≥ 2.

Answer 1

The first five terms of the sequence are -10, -33, -125, -493, -1965

Step-by-step explanation:

The given expression is
`a_n=4a_(n-1)+7`

And
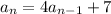
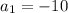`a_1=-10` is the first term of the sequence.

We need to determine the first five terms of the sequence.

Second term:

Substituting n = 2 in the expression
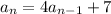`a_n=4a_(n-1)+7`, we have,

`a_2=4a_(2-1)+7`

`a_2=4a_1+7`

`a_2=4(-10)+7`

`a_2=-40+7=-33`

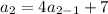
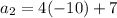
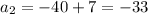
Thus, the second term is -33

Third term:

Substituting n = 3 in the expression
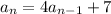`a_n=4a_(n-1)+7`, we have,

`a_3=4a_2+7`

`a_3=4(-33)+7`

`a_3=132+7=-125`

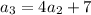
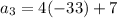
Thus, the third term is -125

Fourth term:

Substituting n = 4 in the expression
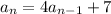`a_n=4a_(n-1)+7`, we have,

`a_4=4a_3+7`

`a_4=4(-125)+7`

`a_4=-500+7=-493`

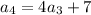
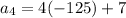
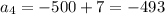
Thus, the fourth term is -493

Fifth term:

Substituting n = 5 in the expression
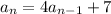`a_n=4a_(n-1)+7`, we have,

`a_5=4a_4+7`

`a_5=4(-493)+7`

`a_5=-1972+7=-1965`

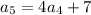
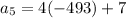
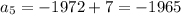
Thus, the fifth term is -1965

Hence, the first five terms of the sequence are -10, -33, -125, -493, -1965