Question

Which can be used to describe the expression? (r^-4)^3 1. There are three factors of r^-4. 2.The expression is equal to 1 over 12 factors of r. 3.Adding the exponents will create an equivalent expression. 4.Multiplying the exponents will create an equivalent expression. 5.The expression simplifies to 1/r^7.

Answer 1

b and d on edge

Explanation:

Answer 2

Option 2) The expression is equal to 1 over 12 factors of r

Option 4) Multiplying the exponents will create an equivalent expression.

Explanation:

We are given the following in the question:

`(r^(-4))^3`

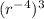
Properties of exponent:

`(x^m)^n = x^(mn)\\\\x^(-a) = (1)/(x^a)`

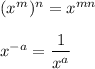
Thus, we can simplify the given expression as:

`(r^(-4))^3\\=r^(-12)\\\\=(1)/(r^(12))`

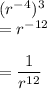
Thus, the correct answer is:

Option 2) The expression is equal to 1 over 12 factors of r

Option 4) Multiplying the exponents will create an equivalent expression.