Answer:
The mountain is 1.34 miles tall.
Explanation:
See the attached diagram.
The height of the mountain is h miles (say).
Now, from the right triangle Δ ABC,
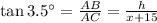
⇒
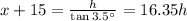 ........... (1)
........... (1)
Again, from the right triangle Δ ABD,
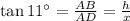
⇒
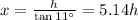 ............. (2)
............. (2)
Now, solving equations (1) and (2) we get,
15 = (16.35 - 5.14)h = 11.2h
⇒ h = 1.34 miles (To the nearest hundredth of a mile)
Therefore, the mountain is 1.34 miles tall. (Answer)