Answer:
After 20 months
Explanation:
This is a compound growth problem which has the formula:
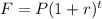
Where
F is future value
P is present amount
r is the rate of growth
t is the time (in months)
Future amount is $65, what he needs at-least
P is the initial amount, that is $10
r is the rate of growth, which is 10% or 10/100 = 0.1
t is time in months, what we need to find
Substituting and solving we get:
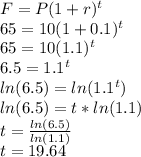
He would need 19.64 months to save up at-least 65. So, that means, he would need 20 months