Question

Write g(x) = –16x + x2 in vertex form. Write the function in standard form. Form a perfect square trinomial by adding and subtractingStartFraction b Over 2 EndFraction squared . Write the trinomial as a binomial squared. Write the function is in vertex form, if needed. G(x) = x2 – 16x b = –16, so StartFraction negative 16 Over 2 EndFraction squared = 64 g(x) = (x2 – 16x + 64) – 64 g(x) = (x – )2 –

Answer 1

Explanation:

I'm not exactly sure what you're asking here, but I do know that to write a polynomial in vertex form you have to complete the square.

In standard form, our polynomial is

`y=x^2-16x`

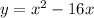
To put this into vertex form, set it equal to 0 first:

`x^2-16x = 0`

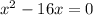
To complete the square, we need the leading coefficient to be a 1 and it is, so we're ready to begin the process of completing the square.

Take half the linear term, square it, then add it into both sides of the equation. Our linear term is 16. Half of 16 is 8, and 8 squared is 64 so we add 64 to both sides.

`x^2-16x+64=64`

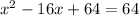
What we have accomplished by doing this is creating a perfect square binomial on the left which is

`(x-8)^2=64`

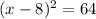
If we want to finish this off properly, we will move the 64 back over by the rest of the equation and set it back equal to y:

`(x-8)^2-64=y`

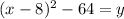
That's vertex form of the polynomial.

Answer 2

g(x) = (x - 8 ) ^2 - 64

Explanation:

just did this