Answer:
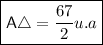
Explanation:
Let's follow up with the solution. Considering a triangle with the vertices
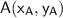 ,
,
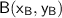 and
and
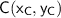 , have a look at the representation in the cartesian plan.
, have a look at the representation in the cartesian plan.
From this representation we can say that the area (A) of a triangle through the knowledge of analytical geometry is given by the determinant of the vertices divided by two, mathematically,
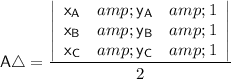
So, applying this knowledge we're going to have,
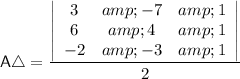
![\mathsf{A} \triangle = (1)/(2)\left[ \left.\begin{array}{ccc} 3 & -7 & 1 \\ 6 & 4 & 1 \\ -2& -3 & 1 \end{array} \right| \begin{array}{cc} 3 & -7 \\ 6 & 4 \\ -2 & -3 \end{array} \right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ifpdesm7xd37yh76mqpvfw3zsnzaufx7tz.png)
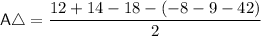
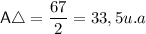
Hope you enjoy it, see ya!)
 Mozambique, Maputo – Matola City – T-3
Mozambique, Maputo – Matola City – T-3
DavidJunior17