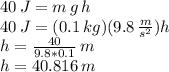Question

The work done on a slingshot is 40.0 joules to pull back a 0.10-kilogram stone. If the slingshot projects the stone straight up in the air, what is the maximum height to which the stone will rise? [Neglect friction.]

Answer 1

The stone reaches a maximum height of approximately 40.816 meters

Step-by-step explanation:

We can use conservation of energy (since we are asked to neglect friction) to solve this problem.

The work done on the slingshot converts into the kinetic energy imparted to the stone, and at a time the kinetic energy is converted into gravitational potential energy as the stone raises in the air.

The maximum potential energy is reached when the kinetic energy is all transferred (stone velocity equals zero).

Recall that the formula for gravitational potential energy is given by: U = m*g*h (where m is the mass of the object, g the local acceleration of gravity (9.8 m/s^2), and h the height reached by the object (our unknown).

So our conservation of energy equation becomes:

`40 \,J=m\,g\,h\\40\,J=(0.1\,kg)(9.8\,(m)/(s^2) )h\\h=(40)/(9.8*0.1) \,m\\h=40.816\,m`

Answer 2

h = 40.76 m

Step-by-step explanation:

given,

Work done on slingshot = 40 J

mass of the stone = 0.1 Kg

maximum height of the stone = ?

work done is equal to change in kinetic energy.

velocity at the maximum speed will be equal to zero

Now,

`40 = (1)/(2)mv^2`

`v=\sqrt{(2(40))/(0.1)}`

`v = 28.28\ m/s`

now, height of the stone

v² = u² + 2gh

0² = 28.28² - 2 x 9.8 x h

h = 40.76 m

maximum height of the stone is equal to 40.76 m.